株式会社ランスモアのホームページへようこそ。

No.567 円孔を有する構造物の曲げ解析における静的陰解法と動的陽解法の比較

　下記の文献を参考にして、解析モデルを作成し、LS-DYNAの静的陰解法と動的陽解法でそれぞれ曲げ変形の解析を行った解析例を示します。解析モデルは、3次元モデルとし、板と治具はそれぞれ六面体ソリッド要素で作成しました。板は弾性体とし、治具は剛体でモデル化しました。圧子と板の間には接触条件を定義して力の伝達を考慮しました。本問題を、ANSYS LS-DYNAの静的陰解法(Static Implicit)と動的陽解法(Dynamic Explicit)による2つの解析手法を用いて解析し、ミーゼスの相当応力分布および最大主応力分布を比較しました。

Fig.4とFig.5より、陰解法と陽解法でそれぞれ得られたミーゼスの相当応力分布はほぼ一致しました。最も応力が大きかった箇所は荷重負荷点近傍でした。

Fig.6とFig.7は、ミーゼスの相当応力の表示レンジを0〜250MPaに絞って描画したコンター図です。工学的に評価したいR部付近に高応力部が発生していることが確認できました。このR部に発生したミーゼスの相当応力の値は、陰解法が388MPa、陽解法が386MPaという結果となりました。

Fig.12とFig.13より、陰解法と陽解法でそれぞれ得られた第1主応力分布はほぼ一致しました。最も応力が大きかった箇所はR部近傍でした。第1主応力の値は、陰解法が392MPa、陽解法が390MPaと正値なので引張応力が作用していることが確認できました。

また、板の先端の荷重負荷点におけるたわみ量は、陰解法が-1.028mm、陽解法が-1.034mmという結果となりました。

なお，本事例はサンプルであることをご了承下さい。

参考文献：泉 聡志，酒井 信介 :理論と実務がつながる実践有限要素法シミュレーション第2版, 森北出版, p.104, 5.3 有限要素法演習問題 中級問題2, 2022

Keywords: 曲げ変形解析，曲げ荷重，接触問題，ミーゼスの相当応力，最大主応力

Tools: LS-PrePost ver.4.11, LS-DYNA MPP Win64 R14.1

July 11, 2025 create a new entry

Fig.1 文献を参考にして作成した解析モデル図(1)

Fig.2 文献を参考にして作成した解析モデル図(2)

Fig.3 メッシュ図

Fig.4 Case001/静的陰解法/ミーゼスの相当応力分布図/ダイナミックレンジ表示

Fig.5 Case002/動的陽解法/ミーゼスの相当応力分布図/ダイナミックレンジ表示

Fig.6 Case001/静的陰解法/ミーゼスの相当応力分布図/固定レンジ表示

Fig.7 Case002/動的陽解法/ミーゼスの相当応力分布図/固定レンジ表示

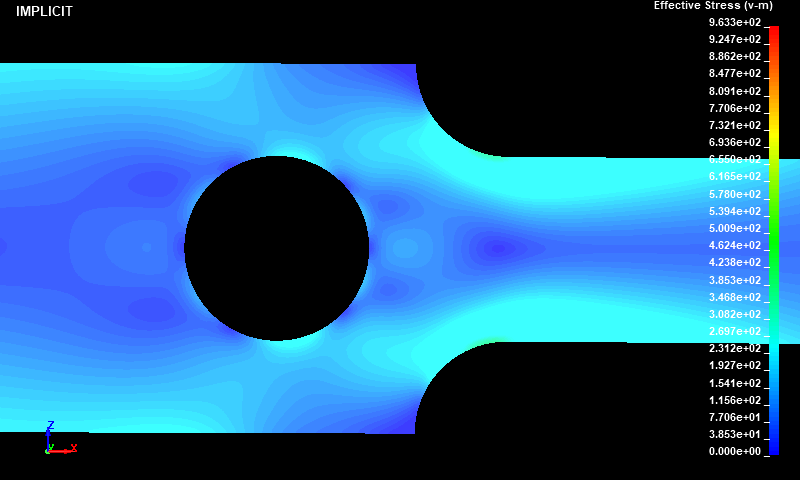
Fig.8 Case001/静的陰解法/ミーゼスの相当応力分布図/ダイナミックレンジ表示/拡大図

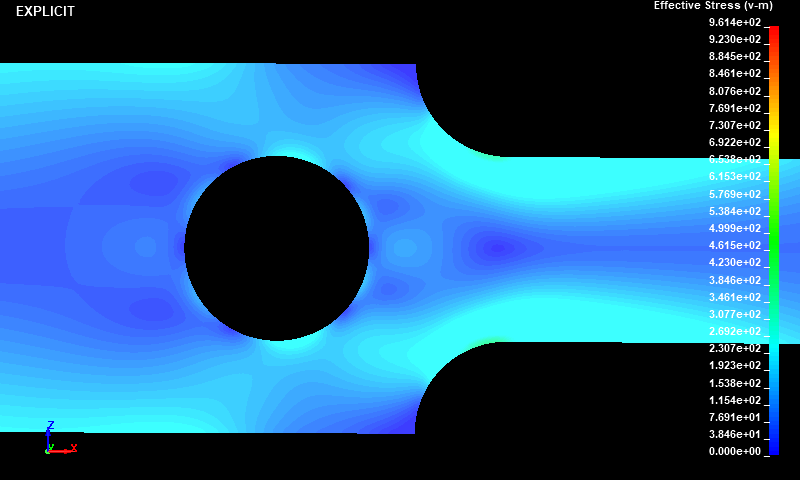
Fig.9 Case002/動的陽解法/ミーゼスの相当応力分布図/ダイナミックレンジ表示/拡大図

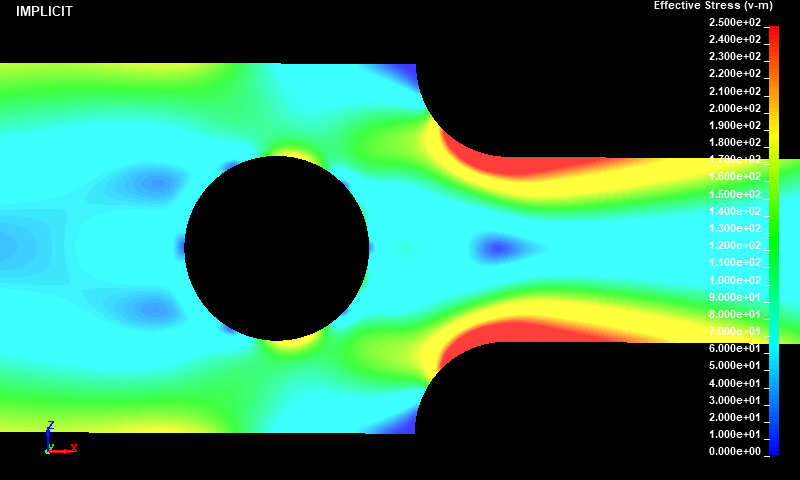
Fig.10 Case001/静的陰解法/ミーゼスの相当応力分布図/固定レンジ表示/拡大図

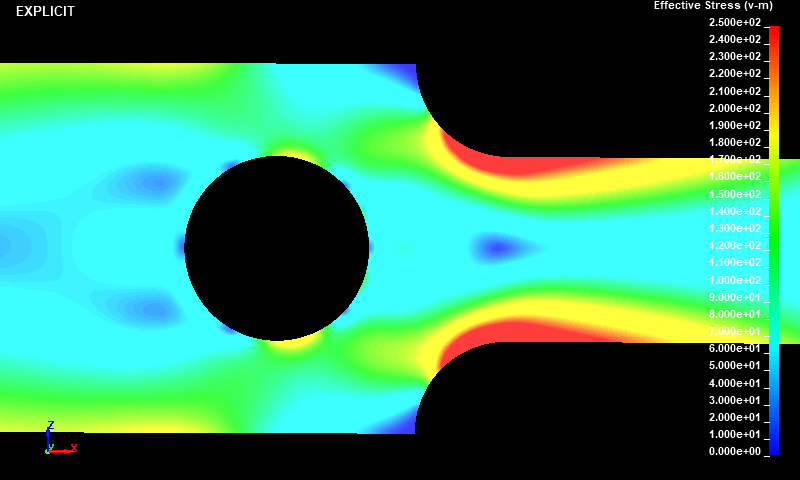
Fig.11 Case002/動的陽解法/ミーゼスの相当応力分布図/固定レンジ表示/拡大図

Fig.12 Case001/静的陰解法/第1主応力分布図/ダイナミックレンジ表示

Fig.13 Case002/動的陽解法/第1主応力分布図/ダイナミックレンジ表示

Fig.14 Case001/静的陰解法/第1主応力分布図/固定レンジ表示

Fig.15 Case002/動的陽解法/第1主応力分布図/固定レンジ表示

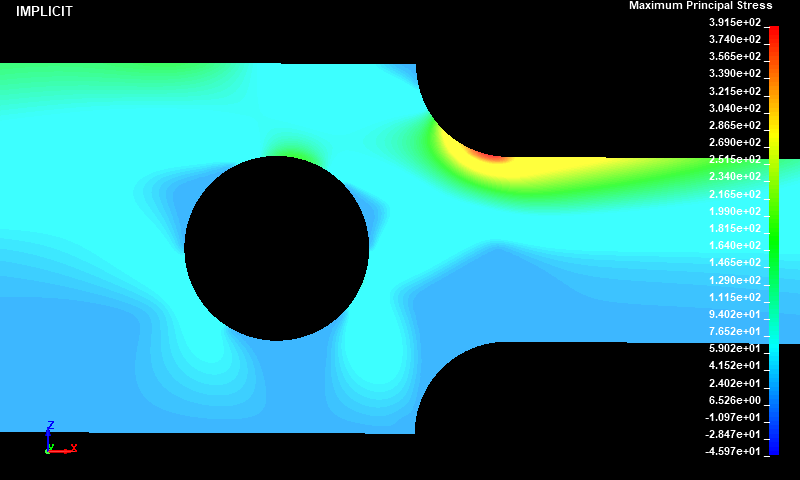
Fig.16 Case001/静的陰解法/第1主応力分布図/ダイナミックレンジ表示/拡大図

Fig.17 Case002/動的陽解法/第1主応力分布図/ダイナミックレンジ表示/拡大図