株式会社ランスモアのホームページへようこそ。

No.568 支柱に固定された梁の曲げ解析における静的陰解法と動的陽解法の比較

　下記の文献を参考にして、解析モデルを作成し、LS-DYNAの静的陰解法と動的陽解法でそれぞれ曲げ変形の解析を行った解析例を示します。

解析モデルは、3次元モデルとして作成しました。

変形の対称性を考慮してモデルは1/2モデルとして作成しました。

梁部分と支柱部分について、要素はすべて六面体一点積分ソリッド要素を用いてメッシュを作成しました。

Fig.1とFig.2に解析モデルの概要を示します。

梁と支柱の材料特性については、文献では線形弾性体としてモデル化していますが、負荷荷重を文献値より大きくした場合に梁の塑性変形が生じる可能性にも対応するために、弊社で作成したSS400の材料データを使用して解析を行いました。

荷重は、文献記載の位置に面圧荷重をLOAD_SEGMENT_SETによって負荷しました。

　本問題を、ANSYS LS-DYNAの静的陰解法(Static Implicit)と動的陽解法(Dynamic Explicit)による2つの解析手法を用いて解析し、X方向応力、ミーゼスの相当応力およびZ方向変位を比較しました。

Fig.3とFig.4に、陽解法と陰解法でそれぞれ得られたX方向応力成分の分布を示します。両者の応力分布はほぼ一致しました。

なお、変形がわかりやすく見えるように変形表示倍率を20倍に設定して可視化してあります。

最大値は支柱と梁の接合部分に生じました。

陽解法の計算における梁の中央部の上端の応力値は -244MPa（圧縮応力）となり、梁の円孔部の中央下端の応力値は +181MPa（引張応力）となりました。

陰解法の計算における梁の中央部の上端の応力値は -243MPa（圧縮応力）となり、梁の円孔部の中央下端の応力値は +181MPa（引張応力）となりました。

これより両者の結果はほぼ一致していることが確認できました。

Fig.5とFig.6に、陽解法と陰解法でそれぞれ得られたミーゼスの相当応力分布を示します。

相当応力の表示レンジは0〜200MPaに絞って描画しました。

梁の中央上端部に最大値が発生し、陽解法の場合は227MPaであり、陰解法の場合は226MPaという結果となり、両者はほぼ一致しました。

梁の円孔部の中央下端部の相当応力の最大値は、陽解法の場合は179MPaであり、陰解法の場合も179MPaという結果となり、両者は一致しました。

Fig.7とFig.8に、陽解法と陰解法でそれぞれ得られたZ方向変位分布を示します。

Z方向変位の最大値は、陽解法と陰解法のそれぞれで梁の中央部にある円孔の上端で最大変位-0.64mmとなり一致しました。梁の中央部の上端での変位も陽解法と陰解法のそれぞれでほぼ-0.64mmという結果となりました。

以上より、本解析例では、動的陽解法の結果と、静的陰解法の結果は一致したと言えます。

なお，本事例はサンプルであることをご了承下さい。

参考文献：泉 聡志，酒井 信介 :理論と実務がつながる実践有限要素法シミュレーション第2版, 森北出版, p.110, 5.3 有限要素法演習問題 中級問題4, 2022

Keywords: 曲げ変形解析，ミーゼスの相当応力，梁のたわみ

Tools: LS-PrePost ver.4.11, LS-DYNA MPP Win64 R16.0

October 11, 2025 create a new entry

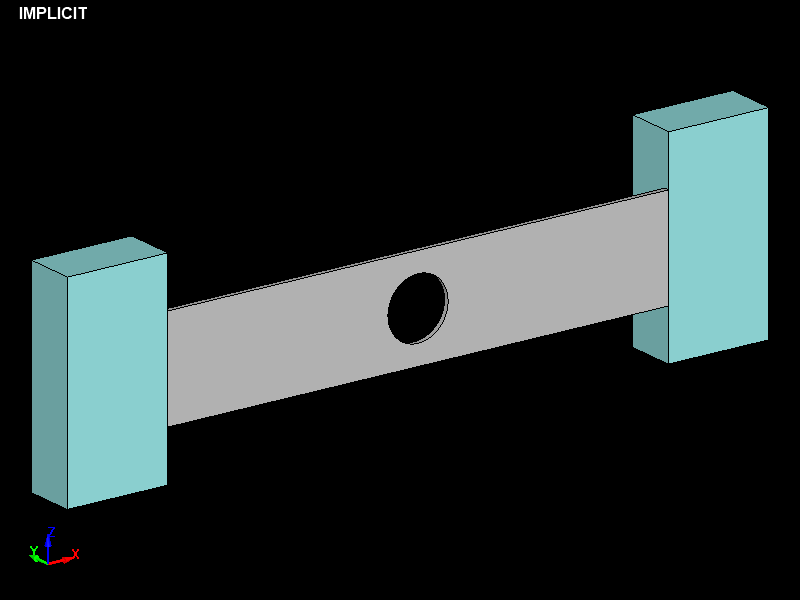
Fig.1 文献を参考にして作成した解析モデル図 対称面側からの視点

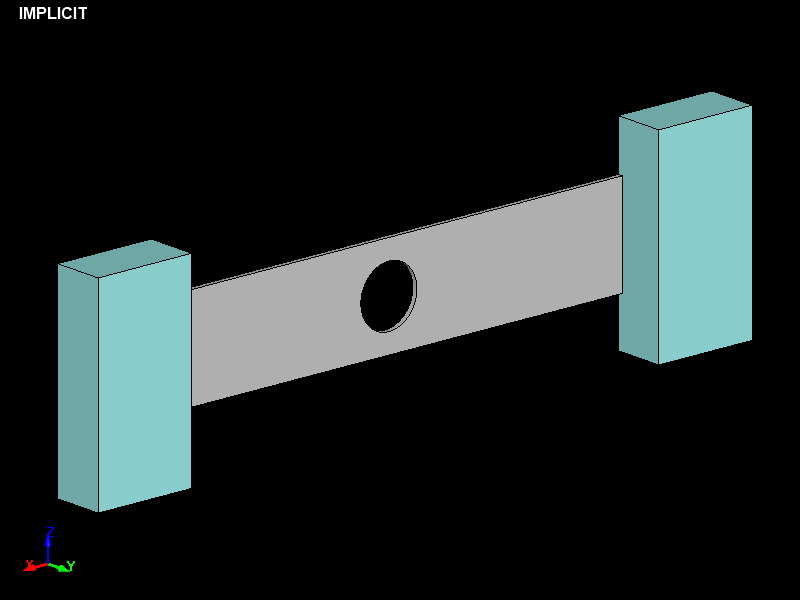
Fig.2 文献を参考にして作成した解析モデル図 外形側からの視点

Fig.3 Case001/動的陽解法/X方向応力成分分布図/固定レンジ表示(-200MPa to 200MPa)

Fig.4 Case002/静的陰解法/X方向応力成分分布図/固定レンジ表示(-200MPa to 200MPa)

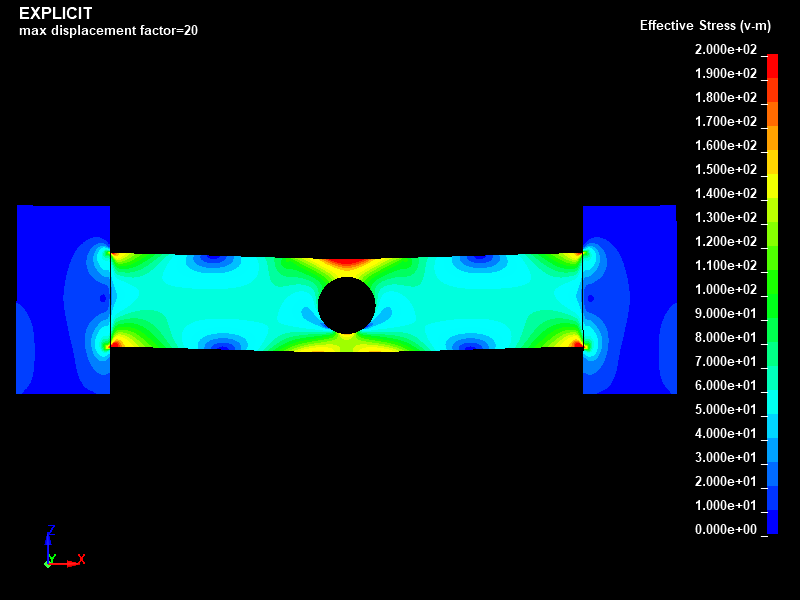
Fig.5 Case001/動的陽解法/ミーゼスの相当応力分布図/固定レンジ表示(0MPa to 200MPa)

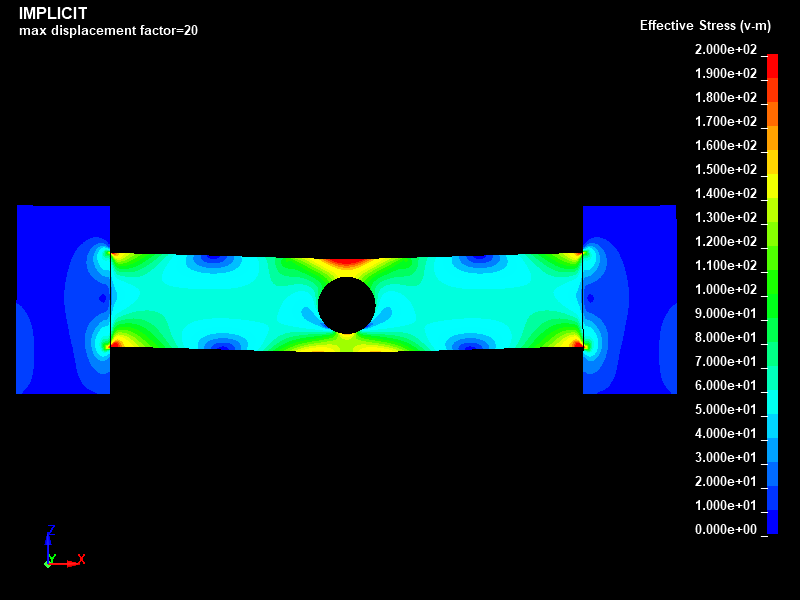
Fig.6 Case002/静的陰解法/ミーゼスの相当応力分布図/固定レンジ表示(0MPa to 200MPa)

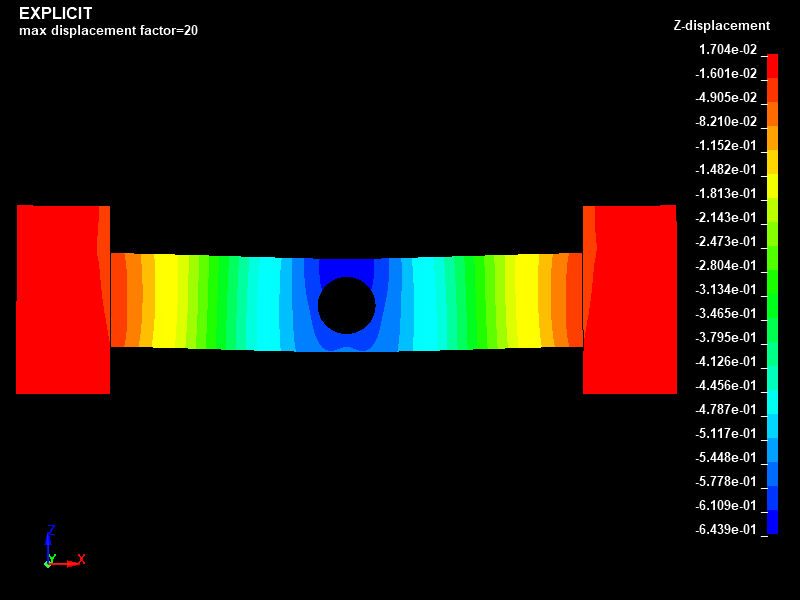
Fig.7 Case001/動的陽解法/Z成分変位分布図/ダイナミックレンジ表示

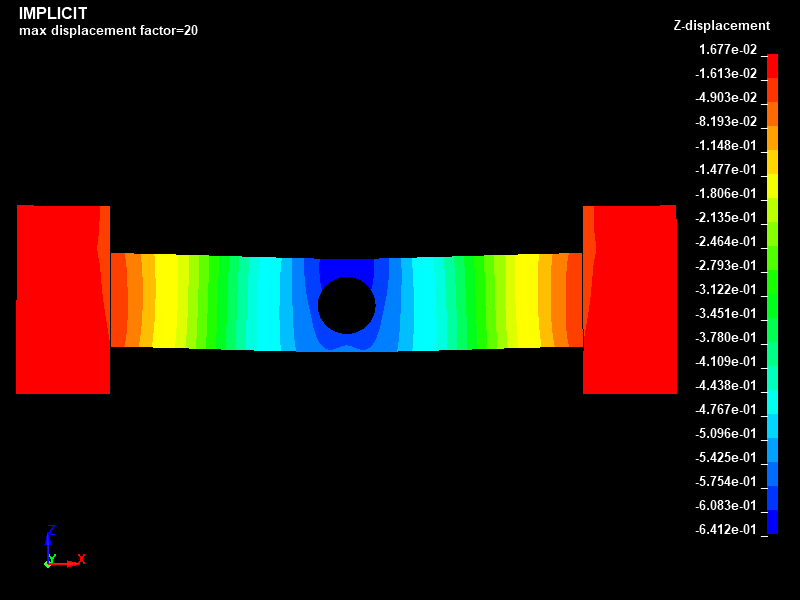
Fig.8 Case002/静的陰解法/Z成分変位分布図/ダイナミックレンジ表示