株式会社ランスモアのホームページへようこそ。

No.565 スタンプの押し込み変形を受ける円柱試験体の応力集中解析

　下記の文献を参考にして、解析モデルを作成し、LS-DYNAの静的陰解法により応力解析を行った解析例を示します。解析モデルは、スタンプと試験体が円柱形状であるので軸対称要素でモデル化しました。スタンプは剛体として、スタンプの上面に押し込み荷重に相当する面圧荷重を負荷しました。スタンプと円柱試験体の間には接触条件を定義して力の伝達をモデル化しました。このときの摩擦係数として0.2を使用しました。本問題は、弾性変形にとどまるため応力集中の問題となり、メッシュ分割数とミーゼスの相当応力の最大値の関係を整理しました。

参考文献：岸 正彦 :例題で学ぶ有限要素法応力解析のノウハウ, 森北出版, p.106, 5.3 スタンプの問題, 2008

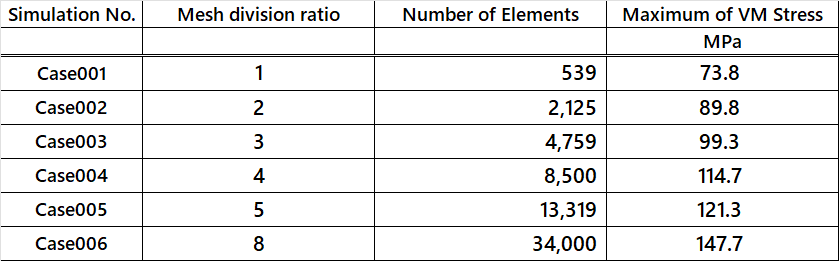
Case001は、半径方向に0mmから26mmまでは13分割し、26mmから50mmまでは6分割としてメッシュ分割にバイアスをかけて作成したケースです。高さ方向には等分割で25分割して作成しました。
Case002は、Case001の2倍に分割数を増やしたケースです。
Case003は、Case001の3倍に分割数を増やしたケースです。
Case004は、Case001の4倍に分割数を増やしたケースです。
Case005は、Case001の5倍に分割数を増やしたケースです。
Case006は、Case001の8倍に分割数を増やしたケースです。

　スタンプの外周部の直下の円柱試験体に応力集中部が発生しました。メッシュサイズが小さくなり、メッシュ分割数が増えるほど、モデルの解像度が向上するため、応力集中部の応力値が高くなっていくことがわかります。ここで、応力集中部のミーゼスの相当応力の最大値は鈍化傾向を示しておらず、メッシュが細かくなるにつれて上昇していきそうな傾向を示しました。

なお，本事例はサンプルであることをご了承下さい。

Keywords: スタンプ, 押し込み解析, 接触問題，応力集中, メッシュ分割, 解像度

Tools: LS-PrePost ver.4.11, LS-DYNA MPP Win64 R14.1

July 07, 2025 create a new entry

Fig.1 Case001のメッシュ分割図

Fig.2 Case002のメッシュ分割図

Fig.3 Case003のメッシュ分割図

Fig.4 Case004のメッシュ分割図

Fig.5 Case005のメッシュ分割図

Fig.6 Case006のメッシュ分割図

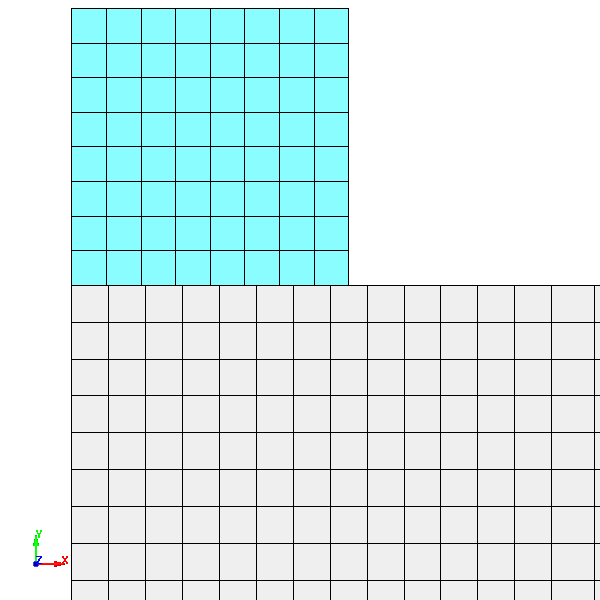
Fig.7 Case001のメッシュ分割図 拡大図

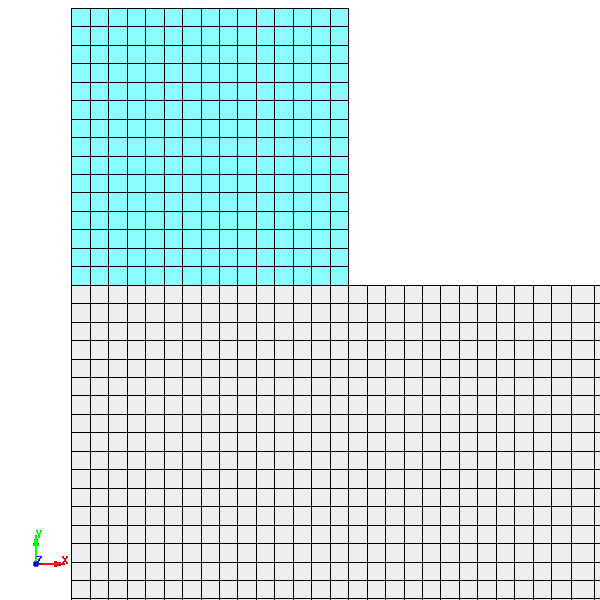
Fig.8 Case002のメッシュ分割図 拡大図

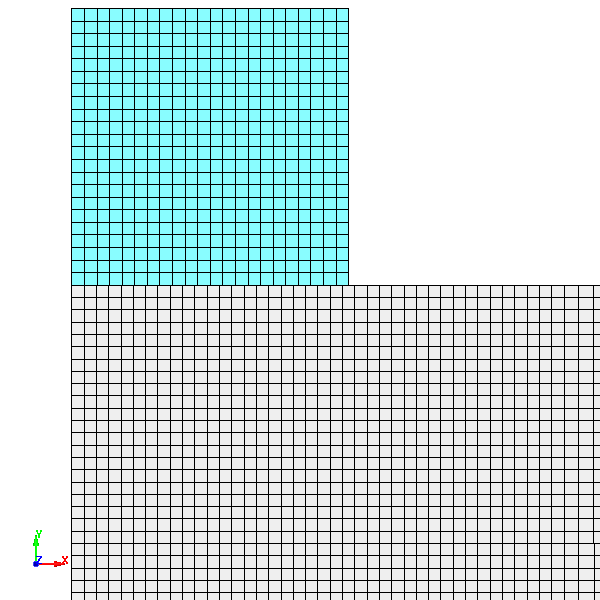
Fig.9 Case003のメッシュ分割図 拡大図

Fig.10 Case004のメッシュ分割図 拡大図

Fig.11 Case005のメッシュ分割図 拡大図

Fig.12 Case006のメッシュ分割図 拡大図

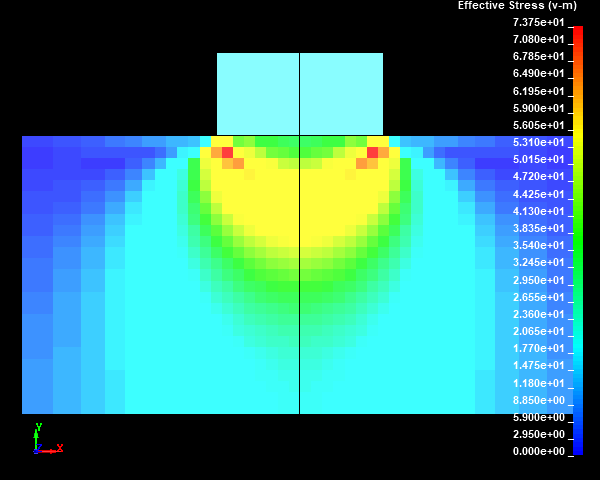
Fig.13 Case001のミーゼスの相当応力分布図(None/ダイナミックレンジ表示)

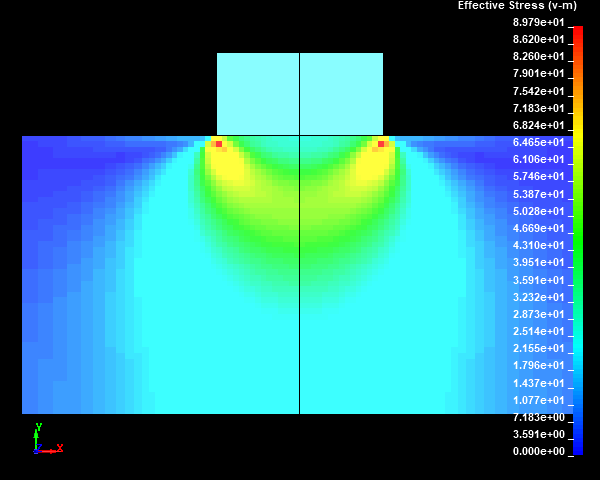
Fig.14 Case002のミーゼスの相当応力分布図(None/ダイナミックレンジ表示)

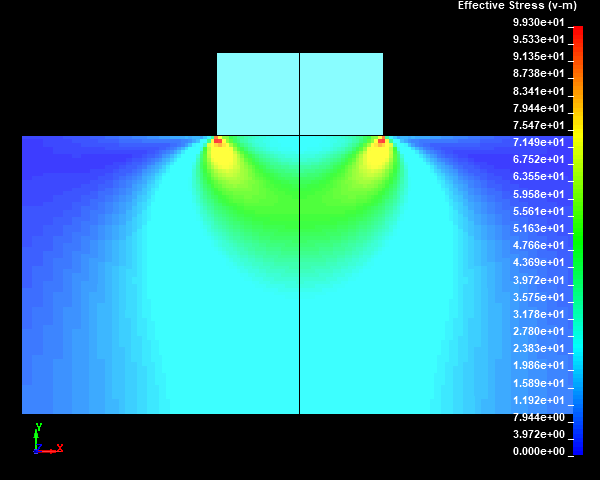
Fig.15 Case003のミーゼスの相当応力分布図(None/ダイナミックレンジ表示)

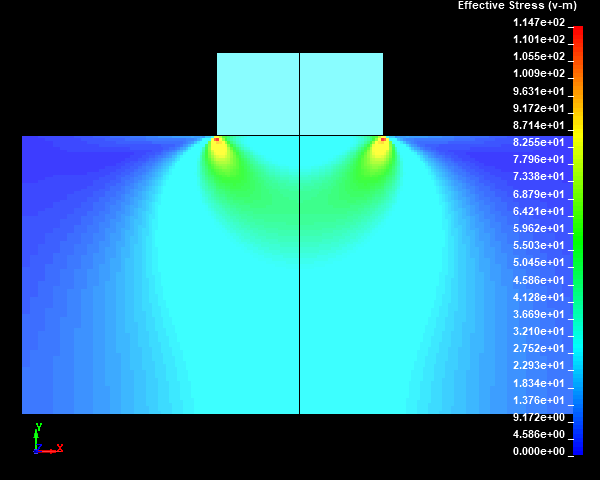
Fig.16 Case004のミーゼスの相当応力分布図(None/ダイナミックレンジ表示)

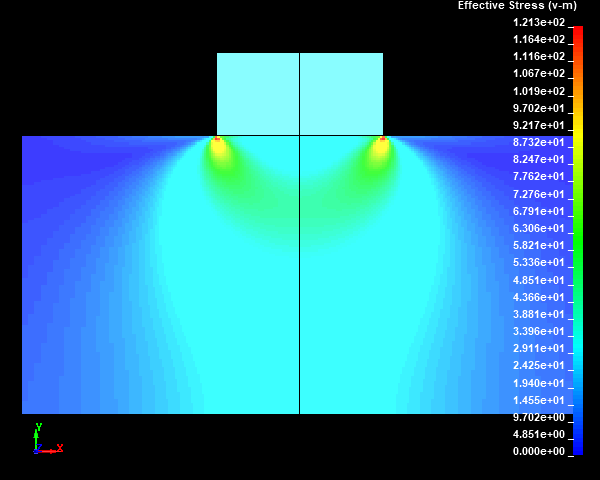
Fig.17 Case005のミーゼスの相当応力分布図(None/ダイナミックレンジ表示)

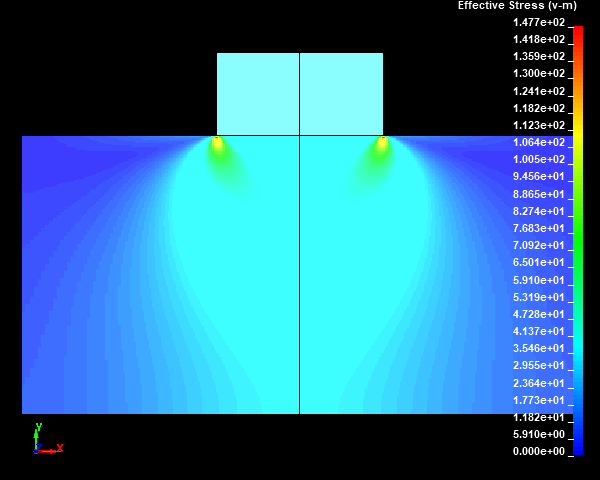
Fig.18 Case006のミーゼスの相当応力分布図(None/ダイナミックレンジ表示)

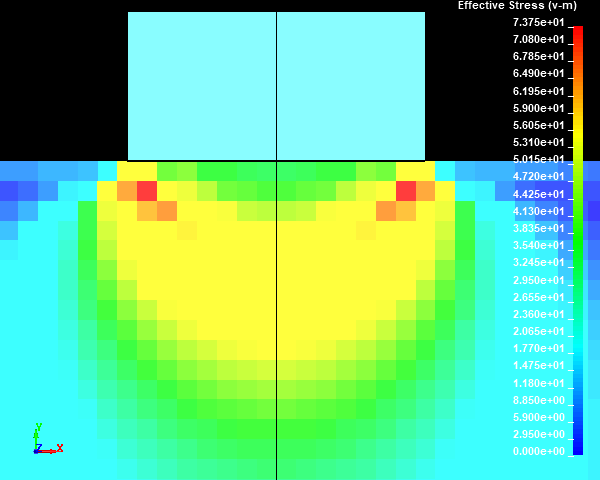
Fig.19 Case001のミーゼスの相当応力分布図 / 拡大図 (None/ダイナミックレンジ表示)

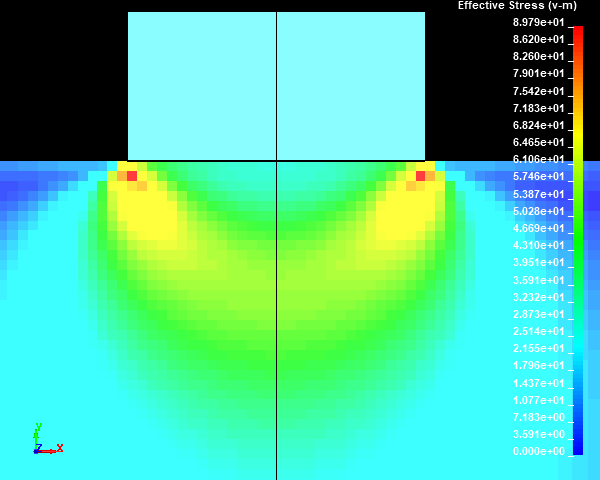
Fig.20 Case002のミーゼスの相当応力分布図 / 拡大図 (None/ダイナミックレンジ表示)

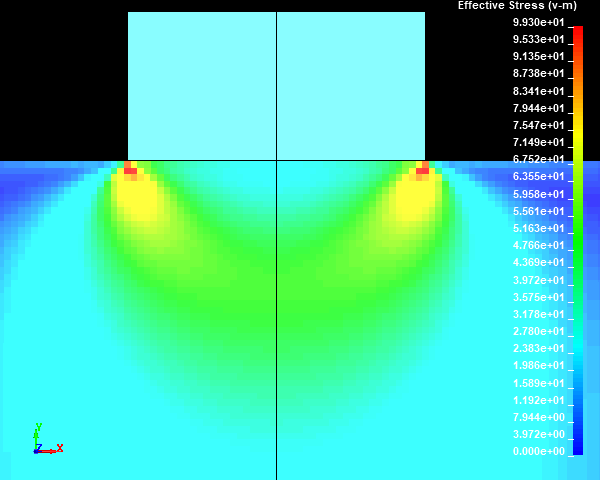
Fig.21 Case003のミーゼスの相当応力分布図 / 拡大図 (None/ダイナミックレンジ表示)

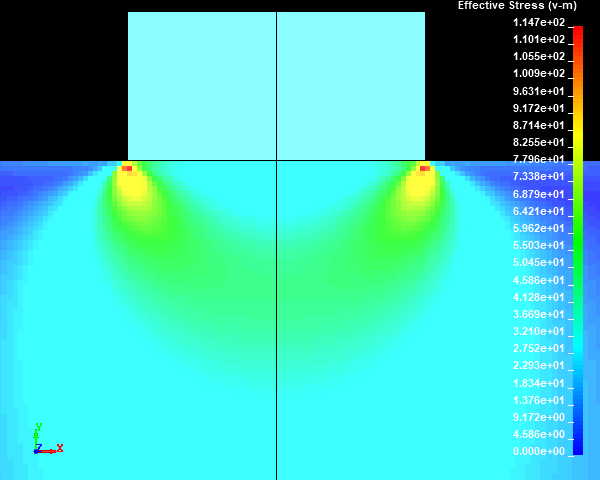
Fig.22 Case004のミーゼスの相当応力分布図 / 拡大図 (None/ダイナミックレンジ表示)

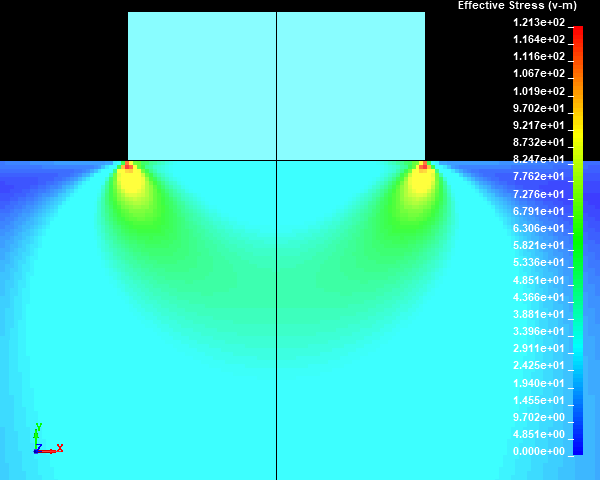
Fig.23 Case005のミーゼスの相当応力分布図 / 拡大図 (None/ダイナミックレンジ表示)

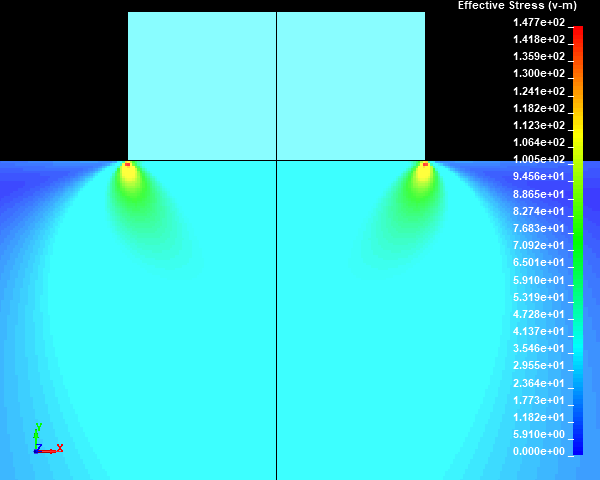
Fig.24 Case006のミーゼスの相当応力分布図 / 拡大図 (None/ダイナミックレンジ表示)

Table.1 解析ケースと相当応力の最大値の一覧表